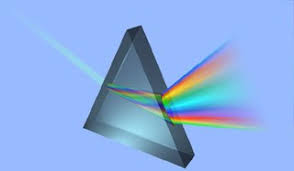
الانحراف في المنشور الثلاثي: زاوية الانحراف. الزاوية الحادة المحصورة بين امتدادي الشعاعين الساقط و الخارج في المنشور الثلاثي

الانحراف في المنشور الثلاثي:

تعريف:

عند مرور شعاع أحادي اللون (λ) عبر منشور ثلاثي، ينحرف عن مساره الأصلي بزاوية انحراف µ نتيجة انكساره مرتين داخل المنشور.

زاوية الانحراف:

تُعرّف زاوية الانحراف (µ) بأنها الزاوية الحادة المحصورة بين امتدادي الشعاعين الساقط والخارج من المنشور.

تتكون زاوية الانحراف من العوامل التالية:

• زاوية رأس المنشور (A): وهي الزاوية بين وجهي السقوط والخروج للمنشور.
• زاوية السقوط الأولى (f1): هي الزاوية بين الشعاع الساقط والسطح الأول للمنشور.
• زاوية السقوط الثانية (f2): هي الزاوية بين الشعاع الساقط والسطح الثاني للمنشور.
• زاوية الانكسار الأولى (q1): هي الزاوية بين الشعاع المنكسر داخل المنشور والسطح الأول.
• زاوية الانكسار الثانية (q2): هي الزاوية بين الشعاع المنكسر داخل المنشور والسطح الثاني.

العلاقة بين زاوية الانحراف والزوايا الأخرى:

يمكن استنتاج العلاقة بين زاوية الانحراف والزوايا الأخرى من خلال هندسة الشكل الرباعي a b c d (شكل رباعي دائري) كما يلي:

A = q1 + f2

f1 - q1 = Ð1

q2 - f2 = Ð2

وبالتالي، يمكن كتابة المعادلة كالتالي:

µ = (q2 - f2) + (f1 - q1)

µ = (f1 + q2) - (q1 + f2)

µ = f1 + q2 - A

بالتالي، يمكن القول أن زاوية الانحراف تساوي مجموع زاويتي السقوط الأولى والثانية ناقص زاوية رأس المنشور.

العوامل المؤثرة على زاوية الانحراف:

تتأثر زاوية الانحراف في المنشور الثلاثي بالعوامل التالية:

• زاوية رأس المنشور (A): كلما زادت زاوية رأس المنشور، زادت زاوية الانحراف.
• زاوية السقوط (f): كلما زادت زاوية السقوط، زادت زاوية الانحراف.
• معامل الانكسار المطلق لمادة المنشور (n): كلما زاد معامل الانكسار، زادت زاوية الانحراف.

تطبيقات انحراف الضوء في المنشور الثلاثي:

تُستخدم ظاهرة انحراف الضوء في المنشور الثلاثي في العديد من التطبيقات، منها:

• منشور نيوتن: وهو أداة بصرية تستخدم لتفريق الضوء إلى ألوانه الطيفية، حيث ينكسر كل لون بزاوية مختلفة داخل المنشور.
• المقاييس: تُستخدم المنشور الثلاثية في بعض أجهزة القياس، مثل مقياس انكسار الضوء، لقياس معامل الانكسار للمواد.
• المناظير: تُستخدم المنشور الثلاثية في بعض المناظير لتحسين جودة الصورة وتقليل الانحرافات.

ملاحظات:

• تعتمد المعادلة المذكورة أعلاه على شعاع أحادي اللون.
• تختلف زاوية الانحراف قليلاً بالنسبة للألوان المختلفة، حيث ينكسر اللون البنفسجي بزاوية أكبر من اللون الأحمر.
• يمكن حساب زاوية الانحراف بدقة باستخدام معادلات أكثر تعقيدًا تأخذ في الاعتبار طول الموجة للضوء.